Northwest Academy of Sciences

Math Battle is an exiting  two-team problem-solving competition. This is a competitions that unites  mathematics, strategy,  sports, team spirits and public performance.  The students benefit from a  math battle in a lot of ways.   They solve problems in a team environment, they get a training in presenting  rigorous mathematical arguments in front of a  qualified jury, and they get a chance to analyze the solutions of their peers for possible gaps and  shortfalls.

Preparation. Each of two teams receives a list of problems, each worth 12 points. They are given a certain amount of time to solve these problem. After the time expires, the teams and the jury gather in some auditorium and the battle begins.

Captains contest. Through a captains contest the jury determines which team goes first. Two team captains are given a simple question which must be answered without consulting the team members. As soon as one captain comes up with the answer, the captains contest is over. If the answer is correct, this captains team wins. Otherwise, other team wins. The winning team decides which of the teams will "issue the challenge". 

• The teams take turn issuing the challenge. Suppose it is now a turn of team A to issue the challenge. Team A declares that they want to hear team B's solution to some problem from the list. Team B can either accept the challenge or decline it.
• If the team B accepted the challenge, then one of the team B members (speaker, or defender) come to the board to explain the solution of the problem. One of the team A members steps forward to act as an opponent. The goal of the speaker is to present a solution. The goal of the opponent is to check the solution, reveal its weak points, or, perhaps, even prove it wrong.
• In both cases, while the speaker explains the solution, the opponent has a right to ask the speaker questions about the solution. At this point, the jury moderates the discussion by cutting off pointless and time consuming questions and arguments. After the speaker has finished his presentation and the opponent has no more questions, the jury may ask the speaker questions about possible errors and unproven points. After the discussion of a solution is finished, the jury distributes the points. Each problem is worth 12 points. Points might be granted to an opponent even if the solution was correct; for example if there were some minor errors pointed by opponent and corrected by the defendant. The jury is also permitted to award points to itself. It awards itself for the
• If team B accepted the challenge (item 2) but it turned out that it's speaker presented a wrong solution (as demonstrated by opponent or determined by jury) then the speaker and the opponent switch places. Now the opponent has a right to present the solution, and the jury acts as an opponent for his presentation.  Jury has a right to award up to 12 point to the opponent in this case.
• If the team B rejected the challenge, then the job of team A is to prove that their challenge was made in correct manner. This means that they delegate a speaker to  present a correct solution to the problem. Team B delegates an opponent to check team A's solution. The solution is presented by team A exactly in the same way as it would have been presented by team B, with one major difference. If it turns out that the team A challenge was not correct , team A is to be punished for buff: team A must challenge team B again.
• If one of the teams runs out of the problems they have solved and is not willing to take changes by challenging the other tea for an unsolved problem, then they can forfeit their right to challenge. In this case, the other team can give the rest of the solutions the have at that moment. The explanations are given as usual, with an opponent present.

Usually, there are 6 to 10 problems in a math battle. Each problem is worth 12 points. Time to solve problems might vary from 30 minutes to a week depending of the problem complexity, level of the players and intentions of organizers.

These Math Battle rules have been ported from "Mathematical Circles (the Russian Experience)" book.  You also might be willing to check the Math Battles section of Toronto Math Circle.

Some examples of our Math Battles:

• Mathematical Battle 1 This is a short battle that is suitable for kids with some experience in problem solving. Preparation time should vary from 40 minutes to 90 minutes depending on the students level and number of students. Actual battle time is about an hour. So the total game lasts for 2-3 hours. (Battle problems adapted from materials of Kirov Summer Math School, Russia).
• Mathematical Battle 2 The April 2009 math battle between our Seniors and Juniors circles..

This contest is very close to gambling. The students participate in such a competition with a great enthusiasm.

The rules are as follows.  Two or more teams of students are given a set of problem of some special type. These are not the traditional math problems that can either be solved or not solved. Math Auction problems are more a research type problems with an easy partial solution that can be improved.

After the problems are submitted to students, they have certain amount of time to solve them. Finally, the auction begins. Each team also receives an equal initial supply of fictional "currency". For example, the initial capital might be 1000 moon dollars. 

Each problem is put up for bid by a teacher. A teacher also declares the total value of the problem. A team that places a winning bid for the problem presents it's solution.  The trick is that every auction problem has a partial solution that can be improved. So if another team believes that  it has a solution with stronger result for the same problem, the problem is put up for auction again. A next buying team presents it's solution. A problem is put up on auction again and again until to team wants to buy a problem any more. When this happens, the team with the best result collects the value of the problem. All the other teams loose their bid money. Now the next problem is put up for auction and so on.

This competition is very motivating for students since the problems are "constructive" - it is easy to find some solution for each problem. The  auctioning aspect and discussion of a winning strategy bring a lot of excitement to the game as well.

At this type of competition, it is important that students have clear understanding of what "stronger solution" means. It is easier to explain the meaning on the examples.

Problem 1. Using only digit 8, arithmetic operations +, -, *, /, brackets and exponentiation, write number 100. Use as little 8's as possible.

Problem 2. Find as many solutions as possible to the following alphanumeric puzzle: BACK+BOA=SCAM

For the first problem, a team should present a solution that uses less 8th then the solution that was presented by the previous team. For the second problem, a team should present at least one solution that was not presented (and written on the board) by the previous teams.

These Math Auction rules have been ported from "Mathematical Circles (the Russian Experience)" book.

Some examples of our Math Auctions:

• Mathematical Auction 1 This is a short auction that is suitable for kids with some experience in problem solving. Preparation time should be approximately 40 minutes. Actual auction takes approximately 40 minutes as well.
• Mathematical Auction 2 March 2009 Auction in our Juniors Circle

This competition is intended for students age 10-12 or older. The game is played by two teams of 4-6 players each. The teacher must have a long list of very simple problems, such that each can be solved in 5 minutes.  At the beginning of the game, use the whiteboard to draw an ice hockey field with the puck placed at the center.

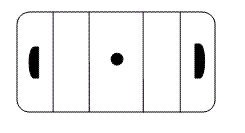
Problems are thrown in one by one. One player per team is invited to solve each problem. The players should rotate. A team should be two problems ahead in order to move a puck one zone close to the direction of opponent's goal posts. Once a puck is in area of goal zone, the goal is scored. The puck is returned to central position, and the game resumes.

It is good idea to play this game after discussing a new topic that needs some practice to soak in. Good examples are: combinatorics, graphs (tests on isomorphic graphs and graphs that can be traced ), algebraic formulas.

These Math Hockey rules have been ported from "Mathematical Circles (the Russian Experience)" book.